Ayooo bermain Quizizz tentang Algoritma dan Pemrograman

 

Explore more at Quizizz.

Read More

BAB I INFORMATIKA DAN PEMBELAJARANNYA

 

Tujuan Pembelajaran 

Pada bab ini, peserta didik akan diajak merefleksikan kembali materi mata pelajaran Informatika kelas VII, dan mendapatkan gambaran umum mengenai materi yang akan dipelajari pada mata pelajaran Informatika kelas VIII. 

Pertanyaan Pemantik 

Apakah kalian sudah pernah mencoba mempelajari Informatika melalui sebuah permainan, baik permainan yang menggunakan komputer maupun tidak? Ceritakan pengalaman kalian dan hal apa yang kalian pelajari dari permainan tersebut!

Peta Konsep 

Apersepsi

Apa yang kalian rasakan setelah mempelajari Informatika pada kelas VII? Menarik, bukan? Ternyata, belajar Informatika tidak selalu harus menggunakan komputer! Justru dengan memerankan diri sebagai komputer atau robot, kita mengalami dan memahami fungsi sistem komputasi. Pada materi kelas VII, kalian sudah belajar bahwa konsep Informatika ternyata dipakai dalam kehidupan kita sehari-hari. Nah, di kelas VIII ini, kalian akan memperdalam pemahaman kalian mengenai Informatika dengan cara yang selaras dengan apa yang kalian alami pada kelas VII, yaitu bahwa mempelajari Informatika ternyata bukan hanya hal praktis menggunakan komputer.

Namun, kalian perlu bermain, mengalami, berpikir, melakukan refleksi, merenung tentang aspek keilmuan yang melatarbelakangi komputer. Yuk, kita lanjutkan petualangan kita untuk belajar Informatika!

Materi

A. Informatika dan Profil Pelajar Pancasila

B. Cara Belajar Informatika

C. Kilas Balik Mata Pelajaran Informatika Kelas VII

D. Apa yang akan Kalian Pelajari di Kelas VIII?

E. Apa Harapan Guru?

F. Pemaknaan dan Kualitas Hasil belajar

G. Refleksi dan Rencana Kegiatan

Read More

LKPD_AI Aktivitas BK-K8-06-U: Teka Teki Operasi Perhitungan

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas BK-K8-06-U: Teka Teki Operasi Perhitungan

Read More

LKPD_AI Aktivitas BK-K8-05-U: Belajar Menyulam

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas BK-K8-05-U: Belajar Menyulam

Read More

LKPD_AI Aktivitas BK-K8-04-U: Konversi Bilangan Biner dan Oktal menjadi Bilangan Desimal

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas BK-K8-04-U: Konversi Bilangan Biner dan Oktal menjadi Bilangan Desimal

Read More

LKPD_AI Aktivitas BK-K8-03-U: Konversi Bilangan Desimal menjadi Bilangan Biner dan Oktal

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas BK-K8-03-U: Konversi Bilangan Desimal menjadi Bilangan Biner dan Oktal

Read More

LKPD_AI Aktivitas BK-K8-02-U: Pupuk Ajaib

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas BK-K8-02-U: Pupuk Ajaib

Read More

LKPD_AI Aktivitas BK-K8-01-U: Mesin Pembentuk Kue

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas BK-K8-01-U: Mesin Pembentuk Kue

Read More

BAB II BERPIKIR KOMPUTASIONAL - D. Struktur Data

Gambar 2.D.1 ilustrasi stack dalam kehidupan sehari-hari

Kalian pasti pernah melihat satu atau lebih tumpukan, misalnya tumpukan buku, tumpukan pakaian, tumpukan piring, dll. Ternyata, konsep dari tumpukan tersebut juga sering digunakan dalam komputer, biasanya disebut stack. Salah satu pemanfaatannya dalam bidang komputer ialah untuk melakukan perhitungan operasi matematika. Menarik, bukan? Ternyata, kita dapat melakukan operasi hitung dengan menumpuk angka-angka (operand) dan simbol-simbol matematika (operator).

Read More

BAB II BERPIKIR KOMPUTASIONAL - C. Algoritma

Dalam kehidupan sehari-hari, tentunya kalian sering menemukan langkah-langkah untuk mencapai sesuatu, misalnya langkah-langkah untuk memasak mi instan. Kumpulan langkah-langkah untuk menyelesaikan sebuah permasalahan itulah yang disebut algoritma.

Read More

BAB II BERPIKIR KOMPUTASIONAL - B. Himpunan dan Sistem Bilangan

Pada bagian B ini, akan dibahas dua hal yang sering digunakan dalam bidang Informatika, yaitu himpunan dan sistem bilangan.

1. Himpunan

Banyak hal dalam kehidupan sehari-hari dapat direpresentasikan dalam bentuk himpunan. Kita dapat mengambil kesimpulan dari pengolahan himpunan. Mari, kita lihat contoh sederhana berikut ini. Adik suka buah jeruk, mangga, dan jambu. Kakak suka rambutan, mangga, duku, dan buah naga. Seseorang bertanya kepada kalian dua buah pertanyaan. Pertanyaan pertama, “Buah apa sajakah yang disukai adik atau kakak?” Pertanyaan kedua, “Buah apa sajakah yang disukai adik dan kakak?”

Tentunya, jawaban kalian berbeda. Untuk menjawab dua buah pertanyaan tersebut, kalian dapat menuliskan himpunan buah kesukaan adik dan kakak. 

Buah kesukaan adik = {jeruk, mangga, jambu}. 

Buah kesukaan kakak ={rambutan, mangga, duku, buah naga}. 

Untuk menjawab pertanyaan pertama, kalian perlu mencari hasil gabungan dari kedua himpunan tersebut yang menghasilkan himpunan baru, yaitu {jeruk, mangga, jambu, rambutan, duku, buah naga}. Untuk menjawab pertanyaan kedua, kalian perlu mencari irisan dari kedua himpunan tersebut, yaitu {mangga}.

Gambar 2.B. 1 Diagram venn buah kesukaan adik dan kakak

2. Sistem Bilangan

Dalam bidang komputer, terdapat empat buah sistem bilangan yang umum digunakan, yaitu sistem bilangan biner (bilangan berbasis 2), oktal (bilangan berbasis 8), desimal (bilangan berbasis 10), dan heksadesimal (bilangan berbasis 16). Dalam kehidupan sehari-hari, bilangan yang pada umumnya digunakan adalah bilangan desimal seperti yang kalian kenal.

a. Ilustrasi Sistem Bilangan

Pada sub-bab ini, kita akan belajar mengenai sistem bilangan dengan bantuan ilustrasi timbangan digital dan tas yang dapat menampung logam mulia.

1) Timbangan Digital

Gambar 2.4 Timbangan Digital

Pernahkah kalian memperhatikan pergantian bilangan-bilangan yang ada pada timbangan digital? Bilangan yang ditunjukkan pada layar timbangan digital pada Gambar 2.4 adalah bilangan desimal (berbasis 10). Mari, kita menyimulasikan dan mempelajari konsep dari bilangan desimal dengan menggunakan bilangan 2789.

Gambar 2.5 Bilangan yang terdiri atas 4 digit

Pada Gambar 2.5, ditampilkan sebuah bilangan yang terdiri atas empat buah angka 0. Dalam sistem bilangan desimal yang berbasis 10, setiap digit pembentuk bilangan tersebut dapat bernilai 0-9. Dalam kasus timbangan digital, jika kalian perhatikan dengan saksama, digit yang pertama akan berubah ketika sebuah benda diletakkan di atasnya adalah digit yang berada pada posisi paling kanan. Digit tersebut akan berubah dari 0, 1, 2, 3, dan seterusnya hingga ada kemungkinan mencapai angka 9 (0009). Jika ternyata bilangan 9 tersebut belum mencukupi, bilangan yang kedua dari kanan akan berubah dari 0 menjadi 1, sedangkan digit paling kanan kembali menjadi 0 (0010). Kemudian, digit paling kanan akan berganti lagi dalam rentang 0 sampai dengan 9. Jika angka 19 ternyata belum mencukupi, digit kedua dari kanan akan berubah menjadi 2 dan digit paling kanan akan berganti menjadi 0 lagi (0020). Hal tersebut terus berlangsung hingga timbangan mencapai angka yang menunjukkan berat dari benda atau timbangan menunjukkan angka maksimalnya dengan 4 digit, yaitu 9999.

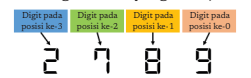
Mari, saat ini, kita pelajari lebih dalam mengenai sistem bilangan desimal. Kita akan menggunakan bilangan 2789, yang ditunjukkan pada Gambar 2.6.

Gambar 2.6 Bilangan 2789 dalam Sistem Bilangan Desimal

Gambar 2.6 menunjukkan posisi setiap bilangan. Posisi dimulai dari posisi ke-0, yang adalah digit paling kanan. Arti lebih mendalam dari Gambar 2.6 dapat dilihat pada Tabel 2.1.

Tabel 2.1 - Contoh Bilangan 2789 dalam Sistem Bilangan Desimal

Tabel 2.1 menunjukkan hubungan antara bilangan yang sedang kita pelajari, yaitu 2789 dengan basis 10 (desimal), posisi setiap digit pembentuk bilangan tersebut, dan basis bilangan. Baris pertama pada Tabel 2.1 menunjukkan penulisan digit-digit pembentuk bilangan. Baris kedua menunjukkan sebutan untuk setiap digit. Baris ketiga menunjukkan posisi setiap digit. Penulisan posisi ini dimulai dari posisi paling kanan, yaitu satuan, dengan nilai awal adalah 0. Baris keempat menunjukkan basis bilangan  dipangkatkan dengan posisi bilangan. Hasil dari perpangkatan inilah yang akan menentukan nilai pengali untuk setiap digit pada bilangan tersebut. Tabel 2.1 menggambarkan cara pembentukan angka 2789 dalam basis 10, yaitu dengan menjumlahkan semua hasil perkalian antara setiap digit dan basisposisi (2000 + 700 + 80 + 9 = 2789).

Nah, apakah kalian pernah membayangkan bagaimana jika batas maksimal setiap digit pada angka timbangan itu bukan angka 9? 

Bagaimana jika setiap digit pada timbangan hanya dapat menunjukkan bilangan 0 atau 1? 

Bagaimana jika setiap digit pada timbangan hanya dapat menunjukkan angka 0 sampai dengan 7? Apakah timbangan tersebut berarti tidak dapat dipakai?

Nah, untuk mempelajari hal ini, kita lihat sebuah kasus mengenai Tas dan Logam Mulia Batang, ya.

2) Tas dan Logam Mulia Batang

Suatu hari, kalian diberi kesempatan untuk membawa sebanyak mungkin logam mulia batang yang tersedia di sebuah ruangan.

Gambar 2.7 Tas dan Logam Mulia

a) Kasus 1

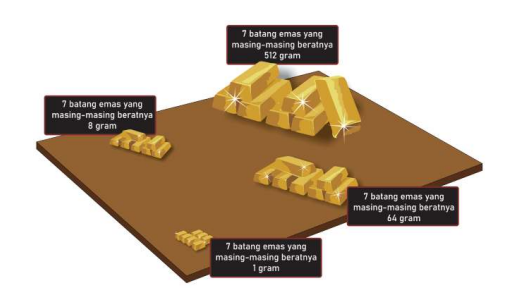
Daftar berat setiap logam mulia batang dan banyaknya logam mulia yang tesedia diberikan pada Gambar 2.8.

Gambar 2.8 Logam Mulia yang Tersedia (Kasus 1) 

Kalian membawa tas yang cukup untuk membawa beban sebesar 2707 gram. Berapa banyakkah logam mulia yang dapat kalian masukkan ke dalam tas? Silakan kalian kerjakan terlebih dahulu soal ini sebelum melihat jawaban yang diberikan.

Jawaban:

Berikut adalah langkah-langkah yang dapat kalian lakukan untuk mengisi tas tersebut.

1. Bilangan terbesar pada kapasitas tas adalah ribuan. Mari, kita lihat ada berapa logam mulia yang beratnya 1000 gram. Ternyata, terdapat 9 batang. Akan tetapi, tentunya, kita tidak dapat membawa semua logam mulia dengan berat 1000 gram tersebut. Tas kita hanya cukup menampung dua batang logam mulia yang masing-masing beratnya adalah 1000 gram.

2. Sisa kapasitas tas kita saat ini adalah 2707 gram - (2 x 1000 gram) = 707 gram.

3. Kita dapat mengisi tas kita dengan tujuh batang logam mulia yang masing-masing beratnya adalah 100 gram.

4. Sisa kapasitas tas kita saat ini adalah 707 gram – (7 x 100 gram) = 7 gram.

5. Karena kapasitas tas hanya 7 gram, kita tidak dapat membawa logam mulia batang dengan berat 10 gram.

6. Sebagai langkah terakhir, kita dapat membawa tujuh batang logam mulia yang masing-masing beratnya adalah 1 gram.

7. Dengan demikian, kapasitas tas kita penuh. Isi tas tersebut dapat dilihat pada Tabel 2.2.

b) Kasus 2

Untuk soal yang sama, bagaimana jika batang logam mulia yang tersedia ukuran dan jumlahnya berbeda? Kapasitas tas tidak berubah, yaitu 2707 gram.

Daftar berat setiap logam mulia batang dan banyaknya logam mulia yang tesedia diberikan pada Gambar 2.9.

Gambar 2.9 Logam mulia yang tersedia (Kasus 2)

Jika dituliskan dalam tabel, ketersediaan logam mulia pada Gambar 2.9 dapat dilihat dalam Tabel 2.3.

Tabel 2.3 Logam Mulia yang Tersedia (Kasus 2)

Berikut adalah langkah-langkah yang dapat kalian lakukan untuk mengisi tas tersebut.

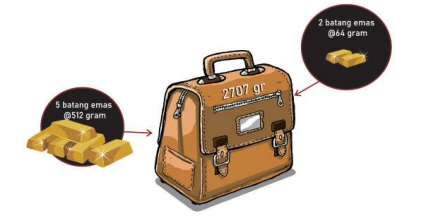
1. Logam mulia paling berat adalah logam mulia dengan ukuran 512 gram. Tas kita mampu menampung 5 batang logam mulia yang masing-masing beratnya adalah 512 gram.

2. Sisa kapasitas tas kita saat ini adalah 2707 gram - (5 x 512 gram) = 147 gram.

3. Kita masih dapat mengisi tas kita dengan dua batang logam mulia yang masing-masing beratnya adalah 64 gram.

4. Sisa kapasitas tas kita saat ini adalah 147 gram – (2 x 64 gram) = 19 gram.

5. Kita masih dapat mengisi tas kita dengan dua batang logam mulia yang masing-masing beratnya adalah 8 gram.

6. Sisa kapasitas tas kita saat ini adalah 19 gram – (2 x 8 gram) = 3 gram.

7. Sebagai langkah terakhir, kita dapat membawa tiga batang logam mulia yang masing-masing beratnya adalah 1 gram.

8. Dengan demikian, kapasitas tas kita penuh. Isi tas tersebut dapat dilihat pada Tabel 2.4.

Tabel 2.4 Isi Tas pada Kasus 2

c) Kasus 3

Untuk soal yang sama, bagaimana jika batang logam mulia yang tersedia ukuran dan jumlahnya berbeda? Kapasitas tas tidak berubah, yaitu 2707 gram. Daftar berat setiap logam mulia batang dan banyaknya logam mulia yang tesedia diberikan pada Tabel 2.5.

Tabel 2.5 Logam Mulia yang Tersedia pada Kasus 3

Langkah untuk menyelesaikan soal ini diberikan dalam Tabel 2.6.

Tabel 2.6 Langkah Penyelesaian Kasus 3

3) Analisis Soal Tas dan Logam mulia Batang dan Kaitannya dengan Timbangan Digital

Soal Tas dan Logam Mulia Batang terdiri atas 3 kasus. Kalian perhatikan hal berikut ini.

a. Pada Tabel 2.2, berat setiap logam mulia adalah bilangan 10n , 0 ≤ n ≤ 3.

b. Pada Tabel 2.4, berat logam mulia adalah bilangan 8n , 0 ≤ n ≤ 3.

c. Pada Tabel 2.5, berat logam mulia adalah bilangan 2n , 0 ≤ n ≤ 11.

Secara tidak langsung, soal ini memperkenalkan kalian pada bilangan berbasis 8 (bilangan oktal) dan bilangan berbasis 2 (bilangan biner). Kapasitas tas yang diberikan tidak berubah, yaitu 270710 atau 2707 dalam bilangan desimal. Pada Tabel 2.4, kalian sedang belajar mengubah bilangan desimal menjadi bilangan oktal. Pada Tabel 2.6, kalian sedang belajar mengubah bilangan desimal menjadi bilangan biner. 

Dengan demikian, berdasarkan: 

• Tabel 2.4, dapat dituliskan bahwa 270710 = 52238. 
• Tabel 2.6, dapat dituliskan bahwa 270710 = 1010100100112

.

Ada beberapa hal yang dapat kita perhatikan dari Tabel 2.2 (tas basis 10), Tabel 2.6 (tas basis 2), dan Tabel 2.4 (tas basis 8), yaitu seperti berikut.

a. Batas bilangan untuk setiap digit dapat dilihat pada Tabel 2.7 berikut ini:

Tabel 2.7 Batas Nilai Digit dalam Sistem Bilangan Desimal, Biner, Oktal

Dengan demikian, jika basis sebuah bilangan kita misalkan dengan variabel n, rentang bilangan dari sebuah digit dalam suatu basis bilangan adalah 0 ≤ n ≤ n-1. Pada soal Tas dan Logam Mulia Batang tersebut, banyaknya balok logam mulia yang tersedia untuk setiap jenis logam mulia (dengan berat yang berbeda) menggambarkan bilangan terbesar dari setiap basis bilangan.

Jika dihubungan dengan cerita timbangan digital (Gambar 2.4), dapat diandaikan, pada bilangan biner, kita memiliki timbangan yang setiap digitnya hanya berisi 0 atau 1.

Adapun pada bilangan oktal, kita memilliki timbangan yang setiap digitnya hanya dapat bernilai 0, 1, 2, 3, 4, 5, 6, atau 7. Proses pergantian digit, sama dengan yang telah dijelaskan pada cerita timbangan digital tersebut, yaitu dimulai dari digit paling kanan.

b. Jika dilihat dari bilangan paling kanan (jika dalam desimal, disebut satuan), terbentuk pola: basis0, basis1, basis2, basis3, ..., basisx

c. Berat batang logam mulia pada setiap tas merepresentasikan basis bilangan, yaitu 10, 2, dan 8.

d. Perhitungan konversi bilangan dari bilangan desimal menjadi bilangan biner atau bilangan oktal, menggunakan bilangan perpangkatan dari basis tertentu, seperti yang tertera pada poin b.

b. Konversi Bilangan Desimal menjadi Bilangan Biner dan Oktal

Nah, pada kasus 2 dan 3 dari kisah Tas dan Logam Mulia Batang, kita dapat melihat bahwa bilangan basis 10 dapat dikonversi menjadi bilangan basis 2 dan 8. Kita tidak perlu melakukan konversi tersebut dengan membayangkan sedang memasukkan logam mulia batang ke dalam sebuah tas dengan kapasitas tertentu. Berikut merupakan langkah-langkah untuk mengonversi bilangn N10 menjadi bilangan basis lain.

1. Buatlah sebuah variabel untuk menampung bilangan hasilnya. Kita misalkan nama variabel tersebut adalah “hasil”.

2. Bagi bilangan N10 dengan basis bilangan yang dituju.

3. Catat sisa hasil bagi dari langkah 2 pada bagian terdepan (paling kiri) dari variabel “hasil”.

4. Ganti bilangan N10 dengan hasil dari langkah 2.

5. Ulangi langkah 2-4 sampai nilai N10 menjadi 0.

Untuk membantu pemahaman mengenai perhitungan konversi bilangan yang berbeda basis, silakan perhatikan Gambar 2.10. Gambar tersebut membantu kalian lebih memahami apa yang dimaksud dengan hasil pembagian dalam bilangan bulat dan sisa hasil bagi.

Gambar 2.10 - Pembagian Bilangan

Sebagai contoh, kita akan mengeksekusi langkah-langkah yang baru saja kalian baca. Kita akan gunakan angka yang sama dengan kasus Tas dan Logam Mulia Batang agar kalian dapat membandingkan hasilnya.

1) Konversi ke Bilangan Biner

Tabel 2.8 Langkah Konversi Bilangan Desimal menjadi Biner

Pada Tabel 2.8, kolom “Nilai Variabel Hasil”, digit yang baru saja ditambahkan adalah digit yang diberi warna merah. Hasil akhir dari tabel tersebut adalah 101010010011. Untuk mempermudah penulisan dan proses baca, pada umumnya, digit-digit pada bilangan biner dituliskan per kelompok dimana setiap kelompok terdiri atas empat digit. Maka: 

101010010011 dapat ditulis menjadi 1010 1001 0011. 

Hasil perhitungan ini sama dengan kasus 3 pada kasus “Tas dan Logam Mulia Batang”, yaitu:

270710 = 1010 1001 00112

2) Konversi ke Bilangan Oktal

Dengan langkah yang sama pada Tabel 2.9, kita akan mengonversi bilangan desimal menjadi bilangan oktal.

Tabel 2.9 Langkah Konversi Bilangan Desimal menjadi Oktal

Dapat dilihat pada Tabel 2.9 bahwa telah ditemukan hasil perhitungan yang sama dengan kasus 2 pada Tas dan Logam Mulia Batang, yaitu 270710 = 52238

Read More

BAB II BERPIKIR KOMPUTASIONAL - A. Fungsi

Dalam pelajaran Matematika, kalian dapat menemukan contoh fungsi, misalnya f(x) = 2x + 3. Fungsi f(x) tersebut akan mengubah nilai input x menjadi nilai keluaran berdasarkan perhitungan 2x + 3. Contoh, jika nilai x adalah 3, maka keluaran dari fungsi tersebut adalah 9 yang didapat dari 2 x 3 + 3.

Dalam kehidupan sehari-hari, kita dapat melihat contoh-contoh penggunaan fungsi. Berikut ini contoh-contoh penggunaan fungsi dalam kehidupan sehari-hari:

a. penulisan teks lagu. 

Dengan format penulisan seperti pada Gambar 2.A.1, bait refrein yang terdiri atas beberapa kalimat tidak perlu diulang-ulang penulisannya. Ketika terdapat kata “Refren” pada teks lagu, pembaca memahami bahwa dia perlu mengulang sebagian tertentu dari teks lagu tersebut.

Gambar 2.A.1 - Struktur Teks Lagu

b. persiapan masuk kelas anak SD

Ketika persiapan masuk kelas untuk peserta didik SD, kalimat yang diucapkan “persiapan masuk kelas” akan terdiri atas tiga kegiatan yaitui: 

• berbaris di depan kelas, 
• pemeriksaan kuku, 
• masuk kelas sesuai urutan baris. 

Setiap pagi, guru hanya perlu mengatakan “persiapan masuk kelas”, peserta didik sudah memahami bahwa mereka perlu melakukan ketiga kegiatan tersebut.

Gambar 2.A.2 Peserta didik SD berbaris memasuki ruang kelas

Sumber: sekolah.data.kemdikbud.go.id 

c. Ibu meminta anaknya untuk membelikan gula

Untuk membeli gula, ibu memberikan uang ke anak dan meminta tolong untuk dibelikan gula. Maka sang anak akan pergi ke warung membawa uang dan kembali membawa gula (beserta uang kembalian, jika ibu memberi uang melebihi harga gula). Karena sang anak sudah SMP dan sudah “teruji” pergi ke warung untuk membeli gula yang diminta ibunya, jadi ibu tidak perlu merinci kewgiatan/kepergian anaknya ke warung. Yang penting, anak berangkat dengan membawa uang dan kembali dengan membawa gula sesuai pesan ibunya, serta uang kembalian jika memang bersisa.

Gambar 2.A.3 Ilustrasi membeli gula di warung

Pada contoh yang ketiga  ini lebih dekat dengan konsep algoritma, dimana ibu memberi kalian instruksi untuk membeli gula, dan karena anak memahami instruksinya, anak dapat melakukannya, yaitu “menukar” uang dengan gula.

Read More

BAB II BERPIKIR KOMPUTASIONAL

 

Tujuan Pembelajaran

Pada bab ini, terdapat konsep-konsep Informatika yang dibungkus dalam bentuk soal cerita yang dekat dengan kehidupan sehari-hari. Secara khusus, pada materi kelas VIII, setelah peserta didik mempelajari materi ini, peserta didik mampu mengidentifikasi algoritma (langkah-langkah) untuk menyelesaikan sebuah masalah, struktur data, representasi data (khususnya bilangan desimal, biner, dan oktal) yang ada di dalamnya.

Pertanyaan Pemantik

Dalam kehidupan sehari-hari, kita sering menjumpai permasalahan dan kita sering menyelesaikan masalah tersebut. Permasalahan yang kita temui tersebut kita selesaikan dengan urutan-urutan langkah sebagai implementasi dari konsep pengenalan pola dan algoritma dalam kehidupan sehari-hari. Dapatkah kalian menyebutkan contoh-contoh implementasi konsep pengenalan pola dan algoritma dalam kehidupan sehari-hari?

Peta Konsep

Gambar 2.1 Peta Konsep Berpikir Komputasional

Apersepsi

Menurut kalian, bagaimana cara kerja komputer sehingga komputer dapat membantu manusia untuk menyelesaikan beberapa masalah dalam kehidupan sehari-hari?

Materi

A. Fungsi

B. Himpunan dan Sistem Bilangan

C. Algoritma

D. Struktur Data

Lembar Aktivitas Peserta Didik

LKPD_AI Aktivitas BK-K8-01-U: Mesin Pembentuk Kue

LKPD_AI Aktivitas BK-K8-02-U: Pupuk Ajaib

LKPD_AI Aktivitas BK-K8-03-U: Konversi Bilangan Desimal menjadi Bilangan Biner dan Oktal

LKPD_AI Aktivitas BK-K8-04-U: Konversi Bilangan Biner dan Oktal menjadi Bilangan Desimal.

LKPD_AI Aktivitas BK-K8-05-U: Belajar Menyulam

LKPD_AI Aktivitas BK-K8-06-U: Teka Teki Operasi Perhitungan

Read More

LAPD_AI Aktivitas TIK-K8-07: Eksplorasi Laboratorium Maya

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas TIK-K8-07: Eksplorasi Laboratorium Maya

Read More

LAPD_AI Aktivitas K8-TIK-06: Menelaah dan Bereksperimen dengan Bacaan Digital

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas K8-TIK-06: Menelaah dan Bereksperimen dengan Bacaan Digital

Read More

LAPD_AK Aktivitas K8-TIK-05: Membuat Laporan Kegiatan dengan Aplikasi Pengolah Kata

Lembar Aktifitas Peserta Didik - Aktivitas Kelompok

Aktivitas K8-TIK-05: Membuat Laporan Kegiatan dengan Aplikasi Pengolah Kata

Read More

LAPD_AK Aktivitas K8-TIK-04: Membuat Laporan Dokumentasi Program dengan Aplikasi Pengolah Kata

Lembar Aktifitas Peserta Didik - Aktivitas Kelompok

Aktivitas K8-TIK-04: Membuat Laporan Dokumentasi Program dengan Aplikasi Pengolah Kata

Read More

LAPD_AI Aktivitas K8-TIK-03: Eksplorasi fitur utama aplikasi pengolah kata

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas K8-TIK-03: Eksplorasi fitur utama aplikasi pengolah kata

Read More

LAPD_AI Aktivitas TIK-K8-02: Eksplorasi Salin dan Tempel pada Aplikasi Perkantoran

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

Aktivitas TIK-K8-02: Eksplorasi Salin dan Tempel pada Aplikasi Perkantoran

Read More

LAPD_AI Aktivitas TIK-K8-01: Eksplorasi Berbagai Format File

Lembar Aktifitas Peserta Didik - Aktivitas Individu 

LAPD_AI Aktivitas TIK-K8-01: Eksplorasi Berbagai Format File

Read More

BAB III TEKNOLOGI INFORMASI DAN KOMUNIKASI - D. Laboratorium Maya

Laboratorium Maya adalah laboratorium yang dibuat secara maya dengan menggunakan komputer. Laboratorium maya memiliki lingkungan interaktif untuk melakukan eksperimen dalam bentuk simulasi. Dengan laboratorium virtual, kalian dapat melakukan eksperimen seperti eksprerimen tentang ilmu pengetahuan alam, matematika, astronomi, geografi, dll. Ketika menggunakan laboratorium maya, kalian seperti bermain dalam permainan (games).

Di sisi lain, laboratorium maya memungkinkan penggunaan yang dilakukan secara bersama. Di saat yang sama, laboratorium maya menjadi lingkungan menyelesaikan masalah bersama yang terdistribusi dan heterogen. 

Para peneliti dapat menggunakannya dalam rangkaian pengerjaan proyek. Laboratorium maya sangat cocok untuk mengeksplorasi sains pada saat kita tidak mempunyai fasilitas yang memadai untuk melakukannya secara riil.

Sejarah

Pada tahun 1977, laboratorium maya pertama hadir dengan nama Virtual Laboratory of Physiology. Pada saat itu, laboratorium maya ini dikembangkan dengan fokus utama pembuatan basis data dengan teks dan gambar. Pada tahun 1998, konsep yang sama masih digunakan dengan modifikasi yang diikuti penggunaan teknologi CD-ROM. Laboratorium ini terus berkembang dari ilmu fisiologi ke ilmu hayat, ilmu pengetahuan umum, seni, dan sastra. 

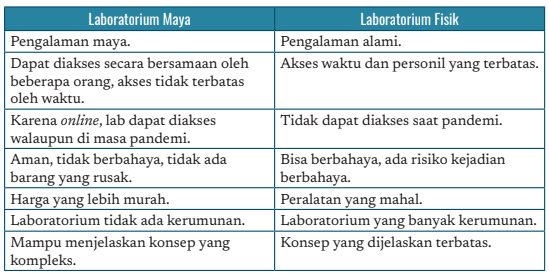
Pada tahun 2000, proyek ini dimasukkan ke dalam proyek penelitian The Experimentalization of Life, yang didanai oleh Volkswagen Foundation. Pada tahun 2002, versi pertama dari Laboratorium Virtual online. Meskipun laboratorium virtual dianggap lebih aman, murah, dan efisien, tetapi masih dianggap memiliki kekurangan. Berikut perbedaan laboratorium maya dengan laboratorium fisik.

Tabel 3.D.1 Perbedaan Laboratorium Maya dan Fisik

Kementerian Pendidikan dan Kebudayaan Indonesia telah memiliki laboratorium virtual (maya) yang dapat diakses di m-edukasi.kemdikbud.go.id/medukasi/?m1=vlab. Laboratorium ini memiliki fitur simulasi praktikum laboratorium yang disajikan secara interaktif dan menarik, dan dikemas dalam lembar kerja dan teori praktikum. Gambar 3.D.1 adalah gambar website laboratorium maya dari kemdikbud.

Gambar 3.D.1 Laboratorium Maya di rumah belajar

Di Internet, tersedia banyak pilihan untuk laboratorium maya. Berikut ini beberapa pilihan laboratorium maya.

1. Laboratorium Maya Phet

Phet adalah salah satu lab maya yang populer untuk simulasi sains. Simulasi Phet tidak berbayar atau gratis. Lab maya ini memiliki fitur yang mudah dalam pencarian dan sangat bagus untuk mata pelajaran IPA.

Ada beberapa review yng menyebutkan bahwa simulasi Phet kurang terstruktur, tetapi ideal untuk inkuiri terpandu. Panduan peserta didik ada dalam bentuk file pdf. Gambar 3.D.2 menunjukkan contoh simulasi balon dan listrik statis.

Phet adalah lab maya yang dikembangkan oleh University of Colorado Boulder, US. Phet dapat diakses di URL https://phet.colorado.edu/

Gambar 3.D.2 Balon dan Listrik Statis

2. NOVA Labs

NOVA labs menawarkan beberapa topik simulasi, yaitu tentang iklim, evolusi, keamanan dunia maya, RNA, awan, energi, atau matahari. Setiap topik memiliki kombinasi video, animasi, wawancara dengan ilmuwan, dan mini-game yang mudah digunakan dan menarik bagi peserta didik. Gambar 3.D.3 menunjukkan contoh simulasi keamanan dunia maya di Nova labs yang dapat diakses di https://www.pbs.org/.

Gambar 3.D.3 Keamanan Dunia Maya

3. The Concord Consortium

Lab maya Concord menyediakan banyak aktivitas STEM interaktif yang selaras dengan Next Generation Science Standard. Lab ini memiliki modul yang dilakukan step by step (langkah demi langkah), mudah untuk digunakan dan dipahami. Salah satu fokus dari modul pada Concord adalah Analisis Data, yang merupakan elemen dari Informatika. Lab maya Concord selalu mengintegrasikan klaim, bukti, dan penjelasan(alasan)nya. Lab maya Concord dapat diakses di https://concord.org. Gambar 3.D.4 menggambarkan simulasi faktor yang mempengaruhi kualitas udara.

Gambar 3.D.4 Simulasi Faktor yang mempengaruhi kualitas udara.

Read More