Pada bagian B ini, akan dibahas dua hal yang sering digunakan dalam bidang Informatika, yaitu himpunan dan sistem bilangan.
1. Himpunan
Banyak hal dalam kehidupan sehari-hari dapat direpresentasikan dalam bentuk himpunan. Kita dapat mengambil kesimpulan dari pengolahan himpunan. Mari, kita lihat contoh sederhana berikut ini. Adik suka buah jeruk, mangga, dan jambu. Kakak suka rambutan, mangga, duku, dan buah naga. Seseorang bertanya kepada kalian dua buah pertanyaan. Pertanyaan pertama, “Buah apa sajakah yang disukai adik atau kakak?” Pertanyaan kedua, “Buah apa sajakah yang disukai adik dan kakak?”
Tentunya, jawaban kalian berbeda. Untuk menjawab dua buah pertanyaan tersebut, kalian dapat menuliskan himpunan buah kesukaan adik dan kakak.
Buah kesukaan adik = {jeruk, mangga, jambu}.
Buah kesukaan kakak ={rambutan, mangga, duku, buah naga}.
Untuk menjawab pertanyaan pertama, kalian perlu mencari hasil gabungan dari kedua himpunan tersebut yang menghasilkan himpunan baru, yaitu {jeruk, mangga, jambu, rambutan, duku, buah naga}. Untuk menjawab pertanyaan kedua, kalian perlu mencari irisan dari kedua himpunan tersebut, yaitu {mangga}.
2. Sistem Bilangan
Dalam bidang komputer, terdapat empat buah sistem bilangan yang umum digunakan, yaitu sistem bilangan biner (bilangan berbasis 2), oktal (bilangan berbasis 8), desimal (bilangan berbasis 10), dan heksadesimal (bilangan berbasis 16). Dalam kehidupan sehari-hari, bilangan yang pada umumnya digunakan adalah bilangan desimal seperti yang kalian kenal.
a. Ilustrasi Sistem Bilangan
Pada sub-bab ini, kita akan belajar mengenai sistem bilangan dengan bantuan ilustrasi timbangan digital dan tas yang dapat menampung logam mulia.
1) Timbangan Digital
Pernahkah kalian memperhatikan pergantian bilangan-bilangan yang ada pada timbangan digital? Bilangan yang ditunjukkan pada layar timbangan digital pada Gambar 2.4 adalah bilangan desimal (berbasis 10). Mari, kita menyimulasikan dan mempelajari konsep dari bilangan desimal dengan menggunakan bilangan 2789.
Pada Gambar 2.5, ditampilkan sebuah bilangan yang terdiri atas empat buah angka 0. Dalam sistem bilangan desimal yang berbasis 10, setiap digit pembentuk bilangan tersebut dapat bernilai 0-9. Dalam kasus timbangan digital, jika kalian perhatikan dengan saksama, digit yang pertama akan berubah ketika sebuah benda diletakkan di atasnya adalah digit yang berada pada posisi paling kanan. Digit tersebut akan berubah dari 0, 1, 2, 3, dan seterusnya hingga ada kemungkinan mencapai angka 9 (0009). Jika ternyata bilangan 9 tersebut belum mencukupi, bilangan yang kedua dari kanan akan berubah dari 0 menjadi 1, sedangkan digit paling kanan kembali menjadi 0 (0010). Kemudian, digit paling kanan akan berganti lagi dalam rentang 0 sampai dengan 9. Jika angka 19 ternyata belum mencukupi, digit kedua dari kanan akan berubah menjadi 2 dan digit paling kanan akan berganti menjadi 0 lagi (0020). Hal tersebut terus berlangsung hingga timbangan mencapai angka yang menunjukkan berat dari benda atau timbangan menunjukkan angka maksimalnya dengan 4 digit, yaitu 9999.
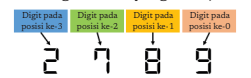
Mari, saat ini, kita pelajari lebih dalam mengenai sistem bilangan desimal. Kita akan menggunakan bilangan 2789, yang ditunjukkan pada Gambar 2.6.
Gambar 2.6 Bilangan 2789 dalam Sistem Bilangan Desimal
Gambar 2.6 menunjukkan posisi setiap bilangan. Posisi dimulai dari posisi ke-0, yang adalah digit paling kanan. Arti lebih mendalam dari Gambar 2.6 dapat dilihat pada Tabel 2.1.
Tabel 2.1 menunjukkan hubungan antara bilangan yang sedang kita pelajari, yaitu 2789 dengan basis 10 (desimal), posisi setiap digit pembentuk bilangan tersebut, dan basis bilangan. Baris pertama pada Tabel 2.1 menunjukkan penulisan digit-digit pembentuk bilangan. Baris kedua menunjukkan sebutan untuk setiap digit. Baris ketiga menunjukkan posisi setiap digit. Penulisan posisi ini dimulai dari posisi paling kanan, yaitu satuan, dengan nilai awal adalah 0. Baris keempat menunjukkan basis bilangan dipangkatkan dengan posisi bilangan. Hasil dari perpangkatan inilah yang akan menentukan nilai pengali untuk setiap digit pada bilangan tersebut. Tabel 2.1 menggambarkan cara pembentukan angka 2789 dalam basis 10, yaitu dengan menjumlahkan semua hasil perkalian antara setiap digit dan basisposisi (2000 + 700 + 80 + 9 = 2789).
Nah, apakah kalian pernah membayangkan bagaimana jika batas maksimal setiap digit pada angka timbangan itu bukan angka 9?
Bagaimana jika setiap digit pada timbangan hanya dapat menunjukkan bilangan 0 atau 1?
Bagaimana jika setiap digit pada timbangan hanya dapat menunjukkan angka 0 sampai dengan 7? Apakah timbangan tersebut berarti tidak dapat dipakai?
Nah, untuk mempelajari hal ini, kita lihat sebuah kasus mengenai Tas dan Logam Mulia Batang, ya.
2) Tas dan Logam Mulia Batang
Suatu hari, kalian diberi kesempatan untuk membawa sebanyak mungkin logam mulia batang yang tersedia di sebuah ruangan.
a) Kasus 1
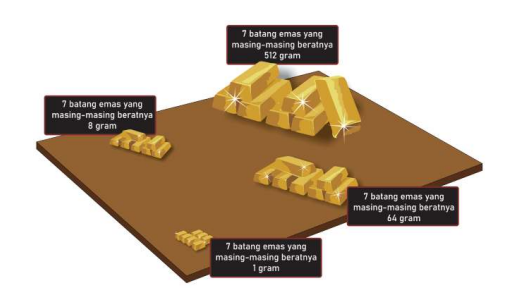
Daftar berat setiap logam mulia batang dan banyaknya logam mulia yang tesedia diberikan pada Gambar 2.8.
Kalian membawa tas yang cukup untuk membawa beban sebesar 2707 gram. Berapa banyakkah logam mulia yang dapat kalian masukkan ke dalam tas? Silakan kalian kerjakan terlebih dahulu soal ini sebelum melihat jawaban yang diberikan.
Jawaban:
Berikut adalah langkah-langkah yang dapat kalian lakukan untuk mengisi tas tersebut.
1. Bilangan terbesar pada kapasitas tas adalah ribuan. Mari, kita lihat ada berapa logam mulia yang beratnya 1000 gram. Ternyata, terdapat 9 batang. Akan tetapi, tentunya, kita tidak dapat membawa semua logam mulia dengan berat 1000 gram tersebut. Tas kita hanya cukup menampung dua batang logam mulia yang masing-masing beratnya adalah 1000 gram.
2. Sisa kapasitas tas kita saat ini adalah 2707 gram - (2 x 1000 gram) = 707 gram.
3. Kita dapat mengisi tas kita dengan tujuh batang logam mulia yang masing-masing beratnya adalah 100 gram.
4. Sisa kapasitas tas kita saat ini adalah 707 gram – (7 x 100 gram) = 7 gram.
5. Karena kapasitas tas hanya 7 gram, kita tidak dapat membawa logam mulia batang dengan berat 10 gram.
6. Sebagai langkah terakhir, kita dapat membawa tujuh batang logam mulia yang masing-masing beratnya adalah 1 gram.
7. Dengan demikian, kapasitas tas kita penuh. Isi tas tersebut dapat dilihat pada Tabel 2.2.
b) Kasus 2
Untuk soal yang sama, bagaimana jika batang logam mulia yang tersedia ukuran dan jumlahnya berbeda? Kapasitas tas tidak berubah, yaitu 2707 gram.
Daftar berat setiap logam mulia batang dan banyaknya logam mulia yang tesedia diberikan pada Gambar 2.9.
Jika dituliskan dalam tabel, ketersediaan logam mulia pada Gambar 2.9 dapat dilihat dalam Tabel 2.3.
Tabel 2.3 Logam Mulia yang Tersedia (Kasus 2)
Berikut adalah langkah-langkah yang dapat kalian lakukan untuk mengisi tas tersebut.
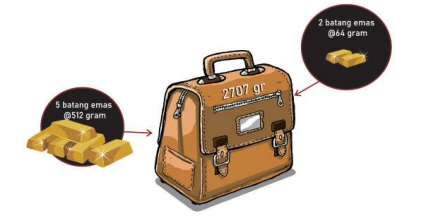
1. Logam mulia paling berat adalah logam mulia dengan ukuran 512 gram. Tas kita mampu menampung 5 batang logam mulia yang masing-masing beratnya adalah 512 gram.
2. Sisa kapasitas tas kita saat ini adalah 2707 gram - (5 x 512 gram) = 147 gram.
3. Kita masih dapat mengisi tas kita dengan dua batang logam mulia yang masing-masing beratnya adalah 64 gram.
4. Sisa kapasitas tas kita saat ini adalah 147 gram – (2 x 64 gram) = 19 gram.
5. Kita masih dapat mengisi tas kita dengan dua batang logam mulia yang masing-masing beratnya adalah 8 gram.
6. Sisa kapasitas tas kita saat ini adalah 19 gram – (2 x 8 gram) = 3 gram.
7. Sebagai langkah terakhir, kita dapat membawa tiga batang logam mulia yang masing-masing beratnya adalah 1 gram.
8. Dengan demikian, kapasitas tas kita penuh. Isi tas tersebut dapat dilihat pada Tabel 2.4.
Tabel 2.4 Isi Tas pada Kasus 2
c) Kasus 3
Untuk soal yang sama, bagaimana jika batang logam mulia yang tersedia ukuran dan jumlahnya berbeda? Kapasitas tas tidak berubah, yaitu 2707 gram. Daftar berat setiap logam mulia batang dan banyaknya logam mulia yang tesedia diberikan pada Tabel 2.5.
Tabel 2.5 Logam Mulia yang Tersedia pada Kasus 3
Langkah untuk menyelesaikan soal ini diberikan dalam Tabel 2.6.
Tabel 2.6 Langkah Penyelesaian Kasus 3
3) Analisis Soal Tas dan Logam mulia Batang dan Kaitannya dengan Timbangan Digital
Soal Tas dan Logam Mulia Batang terdiri atas 3 kasus. Kalian perhatikan hal berikut ini.
a. Pada Tabel 2.2, berat setiap logam mulia adalah bilangan 10n , 0 ≤ n ≤ 3.
b. Pada Tabel 2.4, berat logam mulia adalah bilangan 8n , 0 ≤ n ≤ 3.
c. Pada Tabel 2.5, berat logam mulia adalah bilangan 2n , 0 ≤ n ≤ 11.
Secara tidak langsung, soal ini memperkenalkan kalian pada bilangan berbasis 8 (bilangan oktal) dan bilangan berbasis 2 (bilangan biner). Kapasitas tas yang diberikan tidak berubah, yaitu 270710 atau 2707 dalam bilangan desimal. Pada Tabel 2.4, kalian sedang belajar mengubah bilangan desimal menjadi bilangan oktal. Pada Tabel 2.6, kalian sedang belajar mengubah bilangan desimal menjadi bilangan biner.
Dengan demikian, berdasarkan:
- Tabel 2.4, dapat dituliskan bahwa 270710 = 52238.
- Tabel 2.6, dapat dituliskan bahwa 270710 = 1010100100112
.
Ada beberapa hal yang dapat kita perhatikan dari Tabel 2.2 (tas basis 10), Tabel 2.6 (tas basis 2), dan Tabel 2.4 (tas basis 8), yaitu seperti berikut.
a. Batas bilangan untuk setiap digit dapat dilihat pada Tabel 2.7 berikut ini:
Tabel 2.7 Batas Nilai Digit dalam Sistem Bilangan Desimal, Biner, Oktal
Dengan demikian, jika basis sebuah bilangan kita misalkan dengan variabel n, rentang bilangan dari sebuah digit dalam suatu basis bilangan adalah 0 ≤ n ≤ n-1. Pada soal Tas dan Logam Mulia Batang tersebut, banyaknya balok logam mulia yang tersedia untuk setiap jenis logam mulia (dengan berat yang berbeda) menggambarkan bilangan terbesar dari setiap basis bilangan.
Jika dihubungan dengan cerita timbangan digital (Gambar 2.4), dapat diandaikan, pada bilangan biner, kita memiliki timbangan yang setiap digitnya hanya berisi 0 atau 1.
Adapun pada bilangan oktal, kita memilliki timbangan yang setiap digitnya hanya dapat bernilai 0, 1, 2, 3, 4, 5, 6, atau 7. Proses pergantian digit, sama dengan yang telah dijelaskan pada cerita timbangan digital tersebut, yaitu dimulai dari digit paling kanan.
b. Jika dilihat dari bilangan paling kanan (jika dalam desimal, disebut satuan), terbentuk pola: basis0, basis1, basis2, basis3, ..., basisx
c. Berat batang logam mulia pada setiap tas merepresentasikan basis bilangan, yaitu 10, 2, dan 8.
d. Perhitungan konversi bilangan dari bilangan desimal menjadi bilangan biner atau bilangan oktal, menggunakan bilangan perpangkatan dari basis tertentu, seperti yang tertera pada poin b.
b. Konversi Bilangan Desimal menjadi Bilangan Biner dan Oktal
Nah, pada kasus 2 dan 3 dari kisah Tas dan Logam Mulia Batang, kita dapat melihat bahwa bilangan basis 10 dapat dikonversi menjadi bilangan basis 2 dan 8. Kita tidak perlu melakukan konversi tersebut dengan membayangkan sedang memasukkan logam mulia batang ke dalam sebuah tas dengan kapasitas tertentu. Berikut merupakan langkah-langkah untuk mengonversi bilangn N10 menjadi bilangan basis lain.
1. Buatlah sebuah variabel untuk menampung bilangan hasilnya. Kita misalkan nama variabel tersebut adalah “hasil”.
2. Bagi bilangan N10 dengan basis bilangan yang dituju.
3. Catat sisa hasil bagi dari langkah 2 pada bagian terdepan (paling kiri) dari variabel “hasil”.
4. Ganti bilangan N10 dengan hasil dari langkah 2.
5. Ulangi langkah 2-4 sampai nilai N10 menjadi 0.
Untuk membantu pemahaman mengenai perhitungan konversi bilangan yang berbeda basis, silakan perhatikan Gambar 2.10. Gambar tersebut membantu kalian lebih memahami apa yang dimaksud dengan hasil pembagian dalam bilangan bulat dan sisa hasil bagi.
1) Konversi ke Bilangan Biner
Tabel 2.8 Langkah Konversi Bilangan Desimal menjadi Biner
Pada Tabel 2.8, kolom “Nilai Variabel Hasil”, digit yang baru saja ditambahkan adalah digit yang diberi warna merah. Hasil akhir dari tabel tersebut adalah 101010010011. Untuk mempermudah penulisan dan proses baca, pada umumnya, digit-digit pada bilangan biner dituliskan per kelompok dimana setiap kelompok terdiri atas empat digit. Maka:
101010010011 dapat ditulis menjadi 1010 1001 0011.
Hasil perhitungan ini sama dengan kasus 3 pada kasus “Tas dan Logam Mulia Batang”, yaitu:
270710 = 1010 1001 00112
2) Konversi ke Bilangan Oktal
Dengan langkah yang sama pada Tabel 2.9, kita akan mengonversi bilangan desimal menjadi bilangan oktal.
Tabel 2.9 Langkah Konversi Bilangan Desimal menjadi Oktal
Dapat dilihat pada Tabel 2.9 bahwa telah ditemukan hasil perhitungan yang sama dengan kasus 2 pada Tas dan Logam Mulia Batang, yaitu 270710 = 52238
































0 komentar:
Posting Komentar