BAB IV SISTEM KOMPUTER - B. Pengalamatan Memori

 Pada saat menggunakan komputer, ada kalanya kita perlu menyimpan pekerjaan supaya masih bisa dibuka di waktu yang lain. Proses ini biasanya dilakukan pada perangkat penyimpanan, salah satunya hard disk. Untuk melakukan penyimpanan data, perlu mekanisme yang disebut pengalamatan memroy (memory addressing). Komputer sering menampilkan alamat memori dalam sistem bilangan heksadesimal. Sebelum memahami mekanisme pengalamatan memori, kita harus memahami terlebih dahulu tentang sistem bilangan heksadesimal. Sebaiknya, untuk mempelajari materi ini setelah memahami sistem bilangan yang dibahas dalam unit Berpikir Komputasional buku ini.

1. Sistem Heksadesimal

Sistem heksadesimal menggunakan 16 macam simbol, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C. D, E, dan F. Huruf-huruf A, B, C, D, E, F berturut-turut nilainya adalah 10, 11, 12, 13, 14, 15. Sistem heksadesimal mengorganisasikan memori utama ke dalam suatu byte yang terdiri atas 8 bit (binary digit). Setiap byte digunakan untuk menyimpan satu karakter alfanumerik yang dibagi dalam dua grup setiap bagian 4 bit. Jika satu byte dibentuk dari dua grup 4 bit, setiap bagian 4 bit disebut nibble. Empat bit pertama disebut high-ordernibble dan 4 bit kedua disebut low-order nibble.

Tabel 4.1 Aturan konversi pada Heksadesimal ukuran 4 bit

Contoh:

A16   = 1010             B16  = 1110

1A16 = 2610          1B16 = 2710 

2. Konversi Bilangan

a. Konversi bilangan heksadesimal ke bilangan desimal

Konversi bilangan heksadesimal ke desimal menggunakan perkalian setiap bilangan dengan basis yang dipangkatkan sesuai urutannya, kemudian hasilnya dijumlahkan. Contoh perhitungannya dapat dilihat pada Tabel berikut:

Tabel 4.2 Contoh konversi bilangan heksadesimal ke desimal

b. Konversi bilangan desimal ke bilangan heksadesimal

Konversi bilangan desimal ke hexadesimal dapat dilakukan dengan membagi bilangan desimal dengan 16, hingga tidak bisa dibagi lagi. Contoh perhitungannya dapat dilihat pada Tabel berikut:

Tabel 4.3 Contoh konversi bilangan desimal ke heksadesimal

c. Konversi bilangan biner ke bilangan heksadesimal 

Ketika melakukan konversi bilangan biner ke heksadesimal (16 = 24), setiap 4 angka biner ekuivalen (setara) dengan satu angka heksadesimal. Contoh perhitungannya dapat dilihat pada Tabel berikut:

Tabel 4.4 Contoh  konversi bilangan biner ke heksadesimal

d. Konversi bilangan heksadesimal ke bilangan biner

Untuk konversi bilangan heksadesimal ke biner, setiap 1 angka heksadesimal ekuivalen dengan 4 angka biner. Konversi setiap digit bilangan heksadesimal ke bilangan biner 4 digit, kemudian gabungkan. Jika terdapat digit 0 di depan hasil penggabungan bilangan biner, boleh dihilangkan. Sebagai contoh

001002 = 1002

Contoh perhitungannya dapat dilihat pada Tabel berikut

Tabel 4.5 Contoh  konversi bilangan heksadesimal ke biner

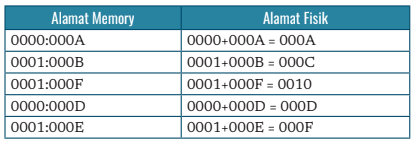
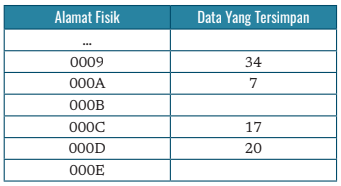
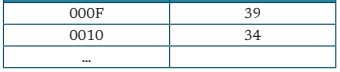
Selain biner, komputer juga menggunakan sistem heksadesimal. Hal ini dilakukan untuk mempersingkat notasi. Sebagai contoh untuk melambangkan bilangan 32 bit ditunjukan pada Tabel berikut:

Tabel 4.6 Contoh konversi bilangan 32 bit

Notasi menjadi lebih singkat karena setiap satu digit tepat menggantikan 4 bit (binary digit). Dengan demikian, 32 bit dapat dinotasikan (dilambangkan) dengan 8 bit saja. Heksadesimal juga lebih mudah digunakan untuk mewakili angka besar. Hanya dibutuhkan dua digit heksadesimal untuk mewakili 256 nilai berbeda, seperti pada Tabel berikut:

Tabel 4.7 Konversi bilangan antara heksadesimal dan biner

Karena setiap digit biner menyimpan tepat 4 bit data, digit heksadesimal dapat dikonversi menjadi 4 digit biner (1 byte) dengan sangat mudah, dan sebaliknya.

3. Pengalamatan Memori dengan Heksadesimal

Alamat memori komputer biasanya ditampilkan dalam bentuk heksadesimal yang digunakan komputer saat menyimpan data. Setiap kali sepotong informasi atau data disimpan, komputer harus menghitung di mana data akan disimpan dalam memori, berdasarkan segmen dan alamat dari hard drive.

Alamat memori ditampilkan sebagai dua bilangan heksadesimal, sebagai contoh 0000:0008. Bilangan heksa yang pertama disebut alamat segmen, sedangkan bilangan kedua disebut alamat offset. Sebenarnya, alamat fisik pada perangkat keras hanya terdiri atas satu bilangan heksadesimal. Namun, untuk memudahkan dalam proses pengaksesan data pada memori agar proses perhitungan akan jadi lebih cepat, digunakan dua bilangan heksadesimal.

Sebagai ilustrasi sederhana, misalnya kita mempunyai data dengan alamat memori sebagai Tabel berikut:

Tabel 4.8 Ilustrasi Penyimpanan Data Pada Alamat Memori Tertentu

Jika dikaitkan dengan matriks, pengalamatan memori dianalogikan sebagai matriks dua dimensi dimana alamat segmen ialah barisnya, sedangkan alamat offset ialah kolomnya sebagai Tabel berikut:

Tabel 4.9 Ilustrasi Penyimpanan Data Pada Alamat Memori Tertentu Sebagai Matriks

Untuk mendapatkan alamat fisik pada data-data tersebut, kita hanya perlu menambahkan nilai bilangan pada alamat segmen dan alamat offset dalam format heksadesimal seperti contoh Tabel berikut:

Tabel 4.10 Ilustrasi Penyimpanan Data Pada Alamat Memori dan Alamat Fisik

Dengan demikian, data-data tersebut akan tersimpan pada alamat fisik perangkat keras penyimpanan sebagai Tabel berikut:

 

Tabel 4.11 Ilustrasi Penyimpanan Data Pada Alamat Fisik